beSmart

From the science disunity to the first steps of its actual integration

From the science disunity

to the first steps of its actual integration

Annotation

In this article the issue has been examined concerning the transfer from disunity of the science to its actual integration. The reason of disunity has been shown, which implies the fact that the surrounding world, first of all, human and society in social-humanitarian sciences are now grasped with the help of general and even to the limit general notions, which are included into the spoken language.

But everything will be set in a different way, if philosophy as its first principles is based on pre-mathematic – comparative notions, which provide with universal formalized language that helps to reveal the initial causative-effective natural and social relations. This is the way to the actual integration of science, when philosophy with its thinking means approaches mathematics, as it used to be at approximately VI century BC in Ancient Greece. That was the exact time when the initial pre-mathematic origins wedded into natural philosophic system, and therefore the physical, ethic, social and religious notions received mathematic coloring.

Key words: Aristotle, Heraclitus, Pre-Socratic, reason, mind, paradigm, identical, diverse, corresponding, opposite, orthogonal.

 

While searching for the final theory, physicians remind dogs rather than eagles: we are scampering and snooping everything around us in search of the beauty traces which we hope to reveal in the laws of the nature but we would hardly be able to see the way to the truth from the top of philosophy¹.

Steven Weinberg

The separation process of the unified field of science into numerous disciplines was named differentiation. This separation allows to know deeper the particular sides of the surrounding world, however it will not let us penetrate into the core of the phenomenon generally. The absence of general bases and general language for the description of the phenomena, studied with the help of sciences, interrupts their interaction.

The classification of sciences in the form of stairs in the hierarchic ladder gives the first steps to the integration. Such structure arranges the separate fragments of the science in a certain order, from the lowest to the highest. Physics as a science that studies the most “simply”- arranged systems, and is situated at the first stair in it. Then the other sciences follow and reflect the animate and inanimate nature and later human and society that give an opportunity to present the hierarchy of natural and humanitarian sciences in the form of certain scheme.

The appearance of new trends that combine previously segmented sciences contributes to the development of integrative tendencies. In such a way the interaction of physics with other branches of knowledge gave birth, for instance, to astrophysics, biophysics, geophysics, and the interaction of chemistry with other sciences led to the appearance of biochemistry, geochemistry, electrical chemistry and others. Moreover, general scientific approaches and methods appear and allow to describe the behavior of different systems in terms of unified mechanism of their development. In this case it concerns ecology and synergetics that allow to justify the formation of ordered stable structures on the basis of self-organization of their elements.

However, the actual integration presumes the deep inter-penetration of sciences on the basis of general principles of the surrounding world cognition which allow to combine different knowledges into a unified system. But this is possible only in case if general structures of mind, generalized notions, used as the “sources” of different branches of knowledge, appear as invariants both in natural and humanitarian sciences.

Therefore, mathematics plays a special role while combining different subject knowledge. It represents the basis, which is crucial for the development of theoretical natural science, as mathematics provides with universal formalized language, with the help of which mankind reveals the causative-effective natural relations. The mathematics reflects the unity in the variety of phenomena, builds models of objects and systems, prognoses their behavior, sets quantitative proportions between objects and their properties.

Likewise mathematics, long before the recognition of its integrative role, philosophy studied comprehension of the world unity and its basic directionality was determined by the intention to reduce to the unified basis the whole changeable variety of not only natural but also social phenomena that was meant to become the most crucial peculiarity of science. But it did not happen. Therefore, the searches of basis for the integration of natural scientific and humanitarian knowledge represent rather serious problem nowadays and there is no theoretical solution so far.

If we rephrase Steven Weinberg, the Nobel laureate in physics, we can name the reason of this problem. It concerns that unlike physicians philosophers started to look for the way to the truth not from the position of dogs but from the position of eagles.

First this tendency declared itself in the studies of Parmenides and Zeno and with the help of Socrates it became dominant in humanitarian thinking nowadays. Its core is that the surrounding world and, first of all, human and society in social-humanitarian sciences started to be comprehended with the help of general and even general to the limit classification notions that are included in the usual spoken language.

Plato secured this “achievement” that finally stalled philosophical thinking. Since that times the philosophy has become abstract-general, definitive, reasonable form of social consciousness, unable to see the way to the truth. And unfortunately there is no other philosophy existing nowadays.

What is the difference between the categories of humanitarian sciences and mathematical abstractions? To my point of view, the first one though they reflect general and even overall but never leave the frames of qualitative diversity of the world. Whereas the mathematical abstractions reflect not qualitative but structural (and quantitative) diversity of the reality, which is determined by the objective causative-effective natural and social relations.

As it turns out the problem of combining the sciences is that philosophy and all humanitarian sciences lost the core of the direction in the intellectual development. Meanwhile the philosophy still represents the methodological basis of science.

But everything could be different if philosophy followed not Plato but Aristotle. What is more, in the dispute with Plato Aristotle does not diverge in choosing the final purpose of philosophy, which is the cognition of the world's unity but nevertheless follows diametrically opposite points of view about the sources of cognition.

In such a way, unlike Plato Aristotle based not on the common but the simplest pre-mathimatic notions of Ancient Greek science which preceded him. Moreover, he based on such notions, which were initial in the process of cognition which grasped not only the parts but the whole creation in general.

As it turns out, the integration of science depends on the ability of human to think not only with the help of mathematic but also pre-mathematic terms, common for the whole science.

A question comes up: can philosophy, which gave birth to the modern science, become a directing force on the way to the complete integration of science? To my point of view, it can if it approaches mathematics with its cognitive means as it used to be in VI century BC in Ancient Greece. Exactly at this time philosophic and mathematic conception started to form with the help of homogeneous characteristics of reasonable thinking process that were qualitatively different from humanitarian mental thinking².

The initial, most abstract sources of pre-mathematics wedded into the natural philosophical system, and therefore physical, ethical, social and religious notions received mathematic color.

The mutual way of philosophy and mathematics that led to their transformation into demonstrative science started from the pre-mathematic sources and numbers which occupy the fundamental place in the system of Ancient Greek ideology. On this basis a new opinion appears that it is possible to express the things with the help of pre-mathematic and mathematic relations. In this relation Greeks were significantly different not only from their predecessors but also from our contemporaries, as pre-mathematic objects were determined as something initial in relation to the existing world. Ionic philosophy is interesting for research while mathematics and philosophy in the works of its representatives interact tightly and in various ways.

Due to the tight connection between general philosophical pre-mathematic ideas and fundamental thesis of mathematics Pythagoras ventured to declare that “the number is the essence of all things”, i.e. he equated in fact mathematics and philosophy. Whereas Aristotle separated distinctly the philosophy that dealt with the pre-mathematic notions (metaphysics) and pure mathematics.

The basis of Aristotle's philosophy was built upon the understanding of pre-mathematic knowledge as the reflection of objective world. These are four kinds of oppositions: “contradictory”, “opposite”, “corresponding”, “privation and possession” and also the first “source” and the last “direction”, which are determined by different kinds of origin and destruction”³. These pre-mathematic origins were grasped by Aristotle as one of the sources of the whole line of devisions' formation in his philosophic system and characterized philosophy as demonstrative science.

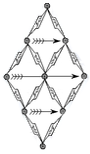
After including “privation and possession” into the notion “corresponding” as its supreme particular case we can mention not four but rather three kinds of oppositions: “contradictory”, “corresponding” and “opposite”. Their interconnection can be presented at the Scheme 1 where the notions “Identical” and “Diverse”, situated at the opposite sides of the scheme, determine Contradictory” as one of three kinds of Aristotle's oppositions.

Scheme 1. Aristotle's paradigm of cognition in our interpretation

The problem of philosophy and other trends of social-humanitarian knowledge is because the notion of “opposition” is now used in wide (Plato's) meaning – as abstract-general notion that includes endless variety of concrete-general meanings. This is the main disadvantage that claims for reasonableness of not only classical dialectics but also social-humanitarian knowledge.

In this relation Aristotle who consolidated with notion of “opposition” only one meaning, as long as he grasped oppositions as “excess” and “deficiency” of one substratum relatively to “intermediate”, occupied the most grounded position. An example can be “bigger” and “smaller” that in relation one to another will be “corresponding” notions, whereas in relation to “intermediate” position they will be “opposites” [2, p.79-86]. A lot of presocratics understood oppositions in such a way and comprehended this relation with the help of a well-known in ancient times “image of scales”. Moreover, most of these philosophers we know thanks to Aristotle.

Another ancient image – is the image of drawing the bow, gave a visual representation of another opposition – orthogonal disposition [3, p. 86-88]; it reveals interrelation of not just one but two interrelated pairs of opposition (dike and adike)⁴.

One of them, a convergent pair (dike) is combined to the ends of the drawing bow. The propagandist of this thinking form in ancient Greece was Heraclitus who suggested in order to comprehend cyclic, i.e. exchange processes, to use such notion as “convergent-divergent”, determined by the harmony of “bow and lira”. Plato exemplifies the words of Heraclitus [DK, Fr. 51 ], who says that “when the single diverges [feuding], it converges with itself [getting on] like the harmony of bow and lira” [4, p.113].

But all the attempts directed at the implication of orthogonal disposition in the social-humanitarian knowledge that reflects the energy of natural and social exchanges (rhythms, cycles, fluctuations, waves) turned to be absolutely unclaimed. “They do not comprehend how a thing agrees being at variance with itself; it is atunement which turns back on itself, like that of the bow and lyre” [DK, Fr. 51].

The reasonable thinking of contemporary humanitarians also rejects this abstraction, while showing thereby its disability to become mental. And the result of this is our contemporaries' disability to think over the way the thinking process was proceeding with Ionics philosophers and later with Aristotle.

At the same time, in order to comprehend society, grasped as the process of resources exchange, it is not enough to use Aristotle's notion “opposite”, as long as not just one but two pairs of opposition (dike and adike), according to Heraclitus, take part in the process of exchange. In common they create more complex notion - “convergent-divergent” that combines two processes into one more complex process (orthogonal), like the “cell” that allows to comprehend all exchange processes and their combination.

If antecedents of Heraclitus and Aristotle applied alternately one origin (dike) or another (adike) in order to comprehend the processes of appearance and destruction, Heraclitus, in contrary, found more complex thinking form, thanks to which he comprehended the world order as the combination of exchanges. “All things are exchanges for fire, and fire for all things, as goods for gold and gold for goods” [DK, Fr.90].

Therefore, wisdom, according to Heraclitus, is “to know everything as the one”, i.e. like complex exchange, like harmony of bow and lira. However, the study of Heraclitus was not understood by his contemporaries and by the time of Plato and Aristotle it was completely forgotten.

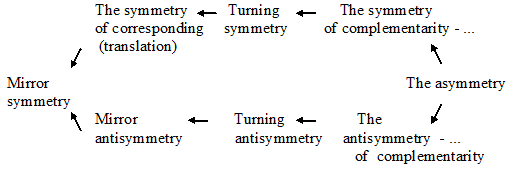
Likewise numerous numbers in arithmetics or notes in music we can build the comparative notions in two parallel lines, and as we cognize the surrounding reality, we supplement them with new notions and each of these notions gives objective point of view at the natural and social world. What is more, all comparative notions build in such a way that each less complex notion represents a particular case (degenerate state) of the more complex notion⁵.

For instance, “Corresponding” and “Opposite” is degenerated condition of such notions as “Orthogonal 1 - Pythagoras” and “Orthogonal 2 - Heraclitus”. And such notion as “Identical” is degenerated condition of “Corresponding” and “Opposite”.

The dots at the scheme represent other not shown comparative notions.

Scheme 2. Universal paradigm of cognition

Likewise on the stairs we will rise from cognition of identical things to the comprehension of their further relation and therefore to the development of more absolute theoretical models that reflect harmony (symmetry) and rationality of the universe, its unity.

Scheme 3. The universal paradigm of cognition as “The theory of everything”

And if “mathematics is the key to the understanding of Universe”⁶ - the first of the most crucial breaks in natural sciences, the most important breakthrough to the integration of science are Aristotle's pre-mathematic notions as kinds of opposition⁷.